📐Hyperbolic Tiling {3,7}

Intro

Here are some documentations on my attempt to generate a hyperbolic tiling. The goal was to set up a system where I can use any texture/video to be displayed inside the tiling. With a bit of creativity, we could then make images in the style of M.C. Escher’s circle limit.

Mission Statement

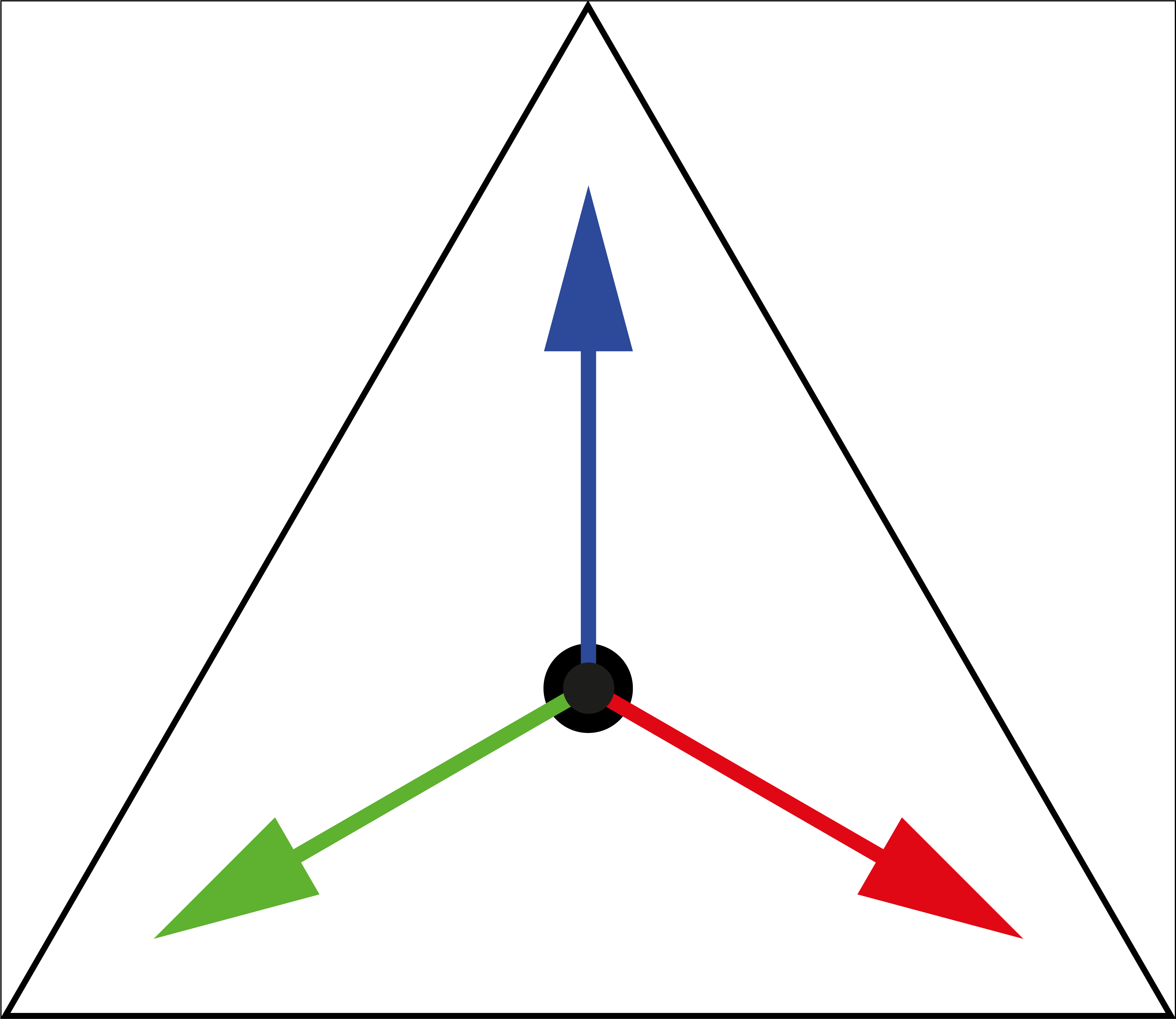
Given any texture of a triangle in the Klein disc model, map it into each triangle of the {3,7} tiling of the Poincaré disk model.

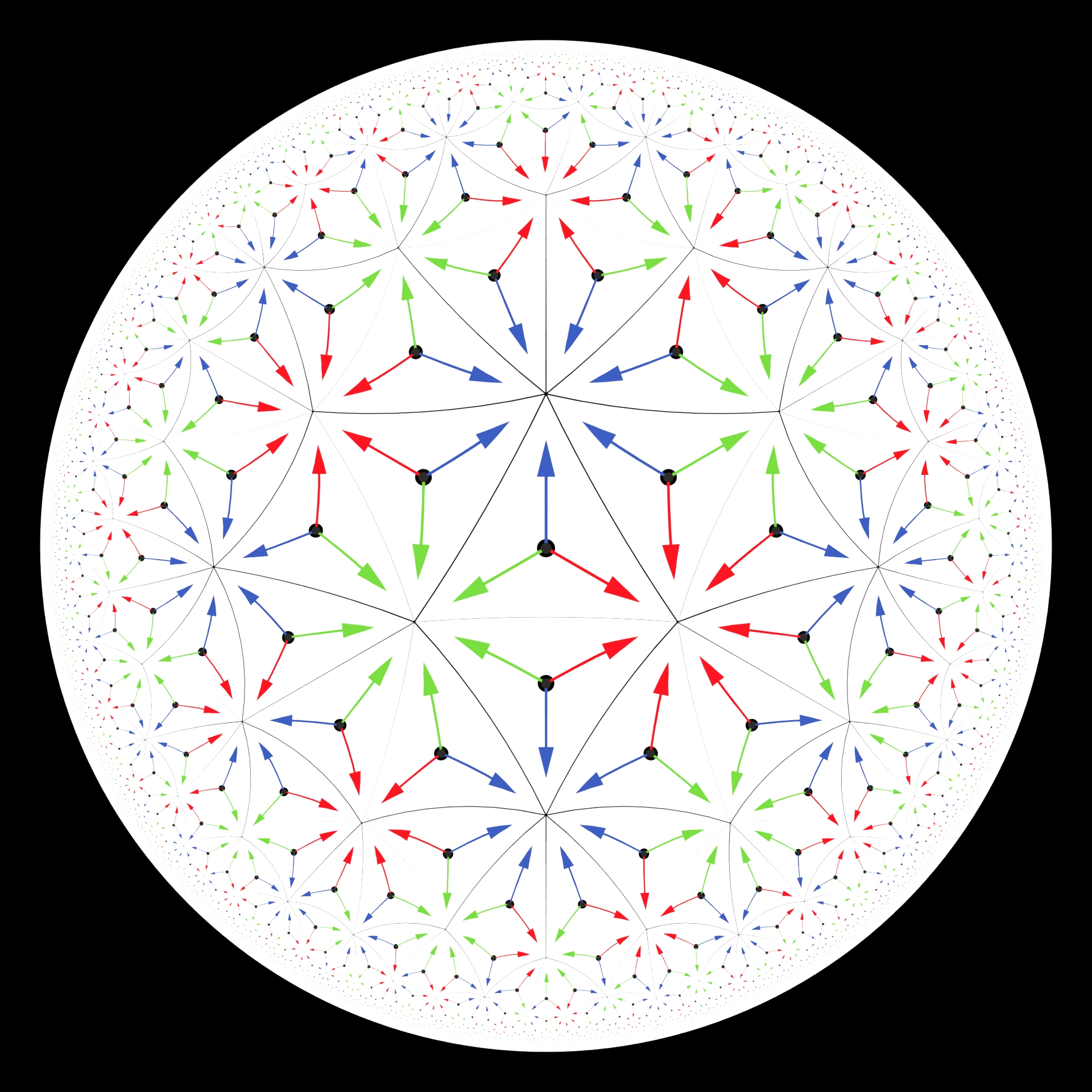
Solution

Create the basic reference mesh for the tiling
Create a refined textured mesh of a single tile
Expand the refined tile using the reference mesh
Place a circle of constant color behind the tiling for fine details at the edge
Be aware of floating point issues near the edge

Results

Notice that the arrow’s colors don’t match up everywhere. There is not much freedom when trying to build a seamless pattern.

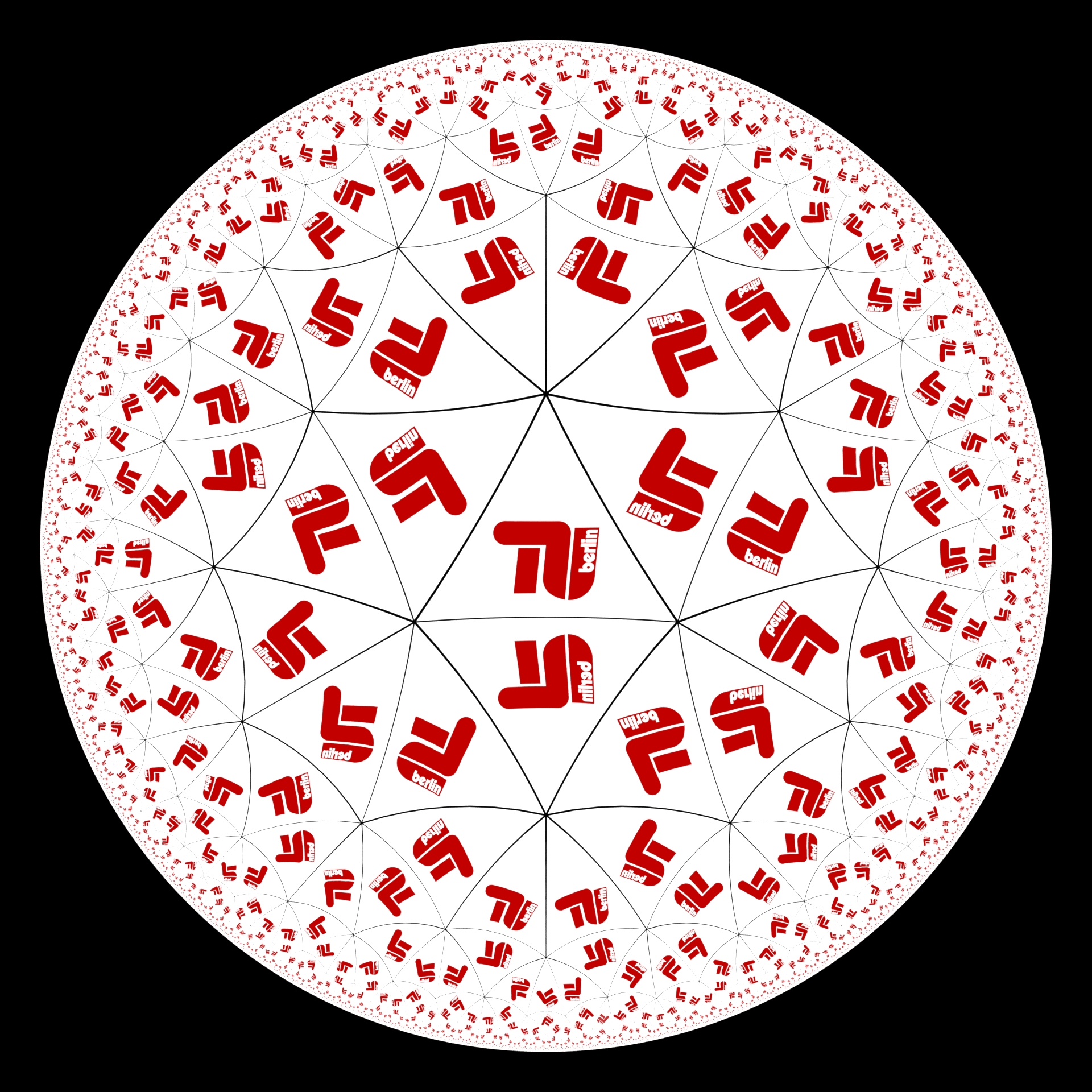
Using the TU logo we get this:

If we stick to radially symmetric textures, we can get quite fancy. Here is some fitting music. Put this on fullscreen and stare at it for a minute.

The clip placed into each triangle:

Notes

There is already a web version of a good tiling generator, but it does not allow us to place the initial image in the straight Klein model setting. These sources were very inspiring for this work: