Zeros of Random Sections on Line Bundles
Bachelor Thesis at TU Berlin (2016). Supervision: Ulrich Pinkall
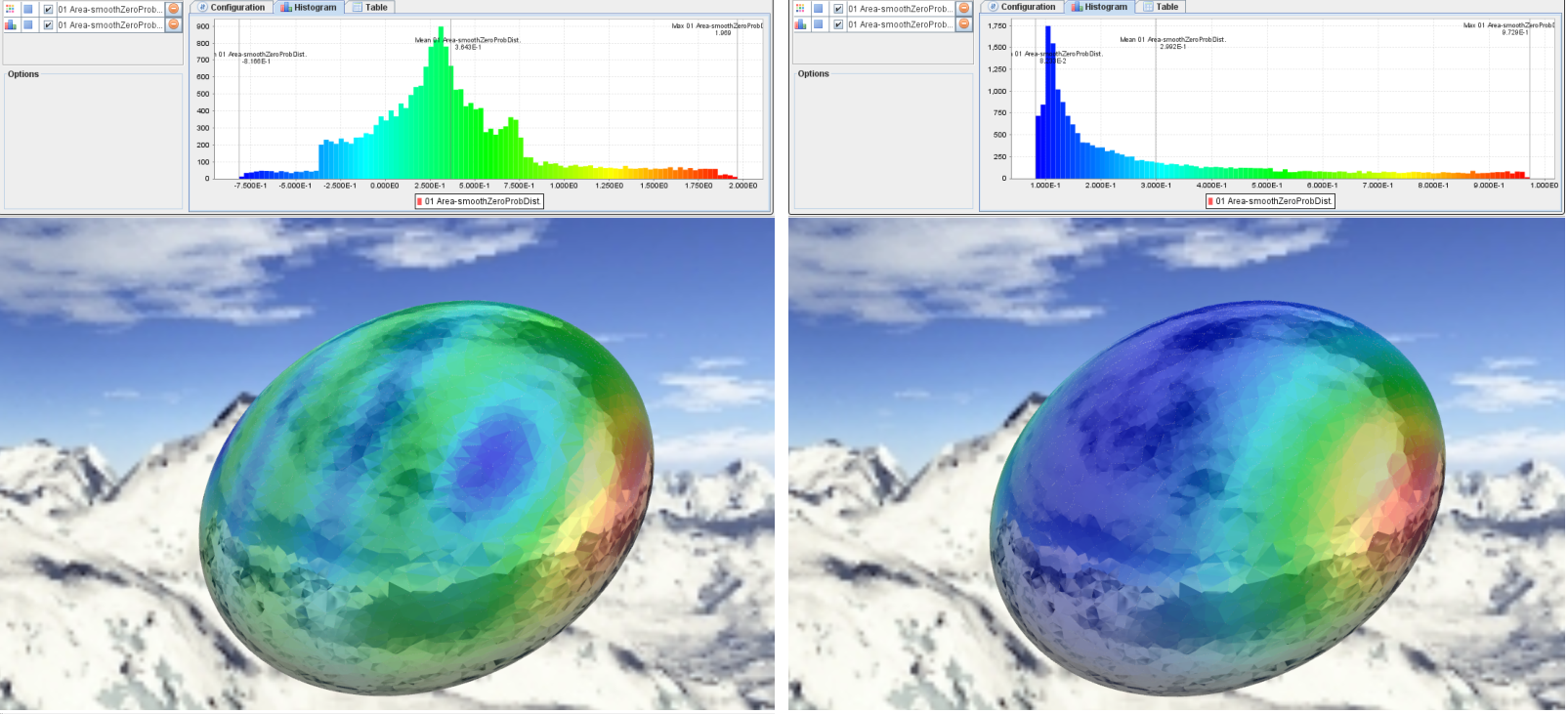
Distribution of the zeros of random vector fields after smoothing.
Left: initial guess of zero distribution for smoothing t=0.
Right: a more accurate distribution of zeros for a larger value of t.
Abstract
Sections of line bundles on 2-dimensional surfaces in 3-dimensional space can have many distinct shapes.
For practical purposes, we prefer smooth sections that are visibly easy to follow. Smoothing operators
have
been developed on discrete surfaces, as seen from Knoppel et al., that can be applied to any section to
return
a smoother section.
The goal of this thesis is to predict the distribution of the smoothed section’s signed zeros with
multiplicity,
generated by applying the smoothing operator to randomly generated sections of Hermitian line bundles on
closed
simplicial complexes. This will be done in a discrete setting, meaning we compute the expected sum of
indices on
each face.
BibTeX
@article{padilla2016randomZeros,
author = {Marcel Padilla},
title = {Zeros of Random Sections on Line Bundles},
journal = {B.S. Thesis},
year = {2016},
month = {06},
publisher = {TU Berlin},
}